728x90
문제

풀이
아니 나는 자연스럽게 2차원배열방식으로 비슷하게 풀었는데 백준 강의 확인해보니까 이걸 또 일차원으로 변형해서 풀수도 있다네?
난 연습단계니까 당연히 그럼 그렇게 해봐야지
저것도 복습일텐데...

음 그럼 2차원배열 방식은 설명 따로 안씀 앞에랑 똑같으니까!
그냥 d[i][j]에서 j에 0 또는 1만 오고 d[i][1]일떄는 d[i-1][0]만 가능한거 조심하면 됨! (1은 연속 불가니까)
이번엔 일차원배열 방식!
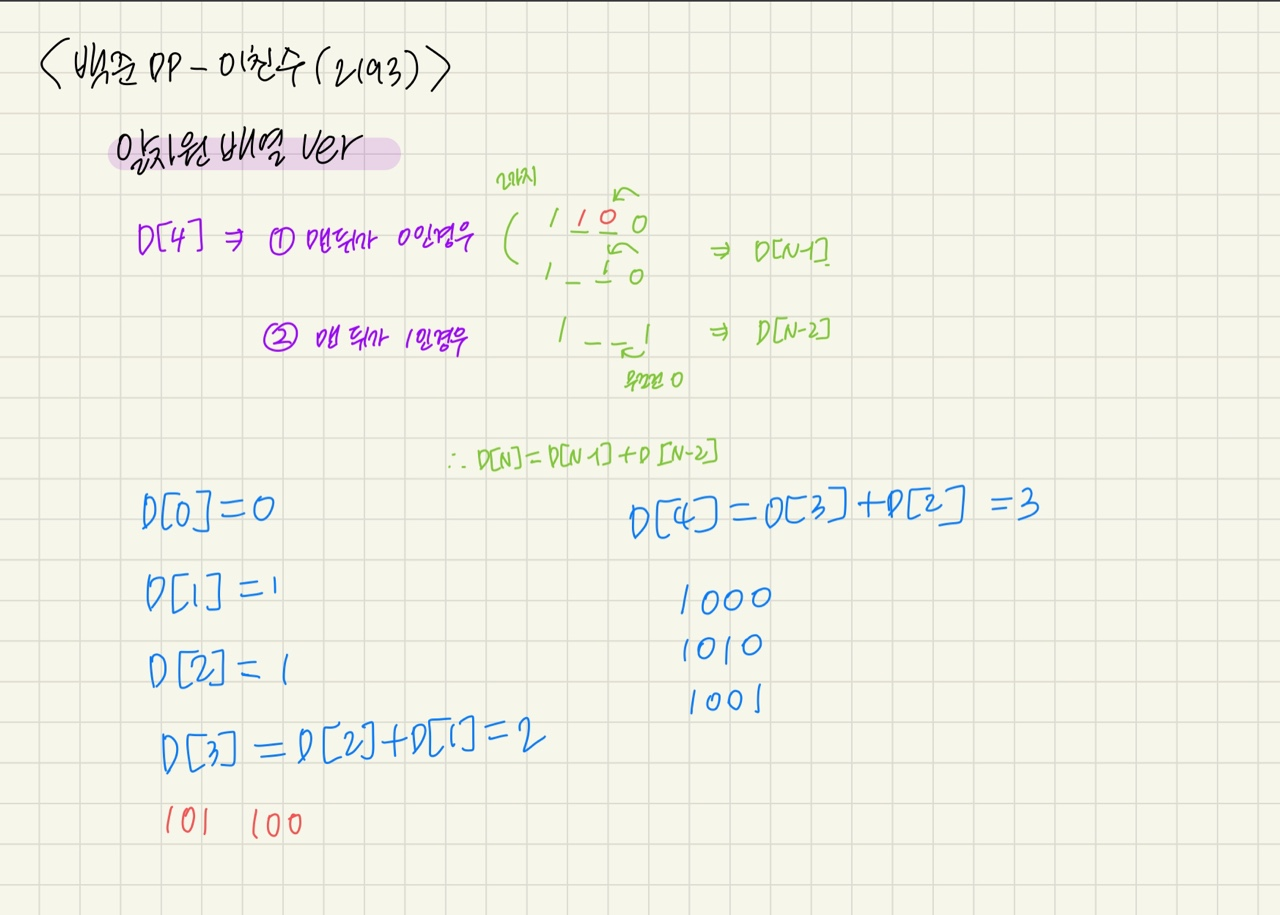
이 방식은 아마 이게 이친수 특성때문에 가능한 것 같아
그리고 이것도 2차원배열이랑 아이디어는 똑같아, 맨 뒤의 숫자가 뭐가 오는지에 따라서 문제를 쪼개가는거야
만약 0이라면? 그 앞에는 0이나 1로 끝나고 길이가 1작은 이친수겠지
근데 1이면? 그 앞에는 무조건 0이 와야되잖아
즉 무슨말이야? 맨 뒤에 1이 오면 그 바로 앞에는 강제로 0이니까 선택지가 존재하지 않아!
그러니까 d[n]에서 맨 뒤가 1이면 d[n]=d[n-2]랑 같다는거지!
1앞에는 바로 0이 와야되니까 길이가 2씩 주는거야~
그래서 d[n]=d[n-1]+d[n-2]가 되는거지!
이해하고 나니까 그렇구나 싶더라!
아래는 코드코드~
코드
이차원 배열 사용한 방식
#include <iostream>
#include <stdio.h>
#define MAX 91
long long d[MAX][2];
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int n;
cin>>n;
d[0][0]=0;
d[0][1]=0;
d[1][0]=0;
d[1][1]=1;
d[2][0]=1;
d[2][1]=0;
d[3][0]=1;
d[3][1]=1;
for(int i=4;i<=n;i++)
{
d[i][0]=d[i-1][0]+d[i-1][1];
d[i][1]=d[i-1][0];
}
printf("%lld\n",d[n][0]+d[n][1]);
return 0;
}
일차원배열로 구현한 방식
#include <iostream>
#include <stdio.h>
#define MAX 91
long long d[MAX];
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int n;
cin>>n;
d[0]=0;
d[1]=1;
for(int i=2;i<=n;i++)
{
d[i]=d[i-1]+d[i-2];
}
printf("%lld\n",d[n]);
return 0;
}728x90
'코딩테스트 > BOJ' 카테고리의 다른 글
| 1157번 단어 공부 (0) | 2021.12.12 |
|---|---|
| 1152번 - 단어의 개수 (0) | 2021.12.11 |
| DP > 오르막 수 (11057번) (0) | 2021.09.04 |
| DP > 쉬운 계단 수 (10844번) (0) | 2021.09.04 |
| DP > 1, 2, 3 더하기 5 (15990번) (0) | 2021.09.04 |




댓글