정신없는 종강 후 정신없이 잉여롭게 살다가 양심의 가책을 느껴서 밀린 강의를 마저 듣기로 했다!
산학도 해야하고 졸작도 해야하고 알바도 해야하고 운동도 해야하지만 틈틈히 그리고 꾸준히 공부해서 코테 준비도 차근차근 하려고 한다!
우선 밀린 백준 강의 마저 듣고...
오늘은 고작 강의 20분 듣고 나가떨어졌지만 시작이 반이니까...(나름 밀린 학교 강의도 듣기 시작함ㅋ_ㅋ)

------------------------------------------------------------------------------------------------------------------------------
<그래프 1 >
- 다이나믹, 브루트포스 알고리즘은 문제를 해결하는 방법 같은 느낌이었다.
- 그래프는 문제의 상황을 그래프로 모델링해서 나타내는 것으로, 알고리즘의 변화는 없고 문제의 상황을 어떻게 그래프로 표현할지가 관건이다.
<그래프>
- 자료구조의 일종으로 정점(vertex, node)와 간선(edge)로 구성된다.
- 간선은 정점간의 관계를 나타낸다.
- G = (V, E)
<그래프 용어 및 설명>
- 경로 : 한 정점에서 다른 정점으로 가는 경로(a->b->c 이런 느낌?)를 의미한다.
- 사이클 : 정점의 시작점과 끝점이 같은 경로
- 단순 경로와 단순 사이클 : 경로/사이클에서 같은 정점을 두 번 이상 방문하지 않는 경로/사이클, 일반적으로 사용한다.
- 방향 있는 그래프 : 간선에 방향이 있는 그래프
- 방향 없는 그래프 : 양방향 그래프, 간선에 방향이 없음
- 두 정점 사이에 간선이 여러 개일 수도 있으며, 두 간선은 서로 다른 간선이다.
- 루프 : 간선의 양 끝 점이 같은 경우
- 가중치 : 간선에 써 있는 어떤 값, 거리, 시간, 비용 등...
- 가중치가 없는 경우에는 1이라고 생각하면 된다.
- 차수 : 정점과 연결되어 있는 간선의 개수
- 방향 그래프의 경우에는 In-degree, Out-degree로 나누어서 차수를 계산한다.
- In-degree : 해당 간선으로 들어오는거, out-degree : 해당 간선에서 나가는 거
- 그래프는 지하철 노선도, 페북&인스타 친구(in-degree, out-degree로 팔로잉 표현), 도로 등에 사용 가능
<그래프의 표현>
- 그래프의 저장 방법에는 인접행렬, 인접 리스트 등으로 표현이 가능하다.
- 이는 효율의 문제이다; 한 정점 X와 연결된 간선으로 효율적으로 찾는 구조가 우선이다.
- 그래프의 표현은 곧 간선의 저장과 같다. (정점은 개수를 숫자로 저장한다.)
<인접 행렬>
- 이차원 배열로 저장하기
- A[i][j] = w(가중치, 없으면 1로), 0(간선이 없는 경우)
- 공간 복잡도 : O(V^2) / 정점 = V, 간선 = E
- 한 개의 정점과 연결된 모든 간선의 개수를 구하는데 걸리는 시간 : O(V)
<인접 리스트>
- 리스트를 이용해서 구현
- A[i] = i와 연결된 정점을 리스트로 포함, 가중치가 있는 경우 가중치도 포함해서 저장
- 리스트는 크기를 동적으로 변경할 수 있어야 함
- 연결리스트나 라이브러리 함수 사용(C++ : vector, python : [ ])
- 공간 복잡도 : O(E)
- 한 정점과 연결된 모든 간선을 찾는 시간 : O(차수)
<(u,v) 간선의 존재 여부 찾기>
- 인접 행렬 : O(1)
- 인접 리스트 : O(차수)
<간선 리스트>
- 배열을 이용해서 구현하며, 간선을 모두 저장한다.
- 라이브러리의 제한으로 연결리스트를 사용해서 구현해야 하는데 그러기 싫을 때(?) 쓰는 자료구조
- 순서
1. 간선을 모두 1차원 배열(벡터)에 저장한다.
2. 각 간선의 앞 정점을 기준으로 정렬한 후 개수를 센다. (각 정점에서 출발하는 간선의 개수 count)
3. 앞에서부터 차례대로 더해준다.


4. i번 정점과 연결된 간선은 간선을 저장한 배열에서 cnt[i-1]부터 cnt[i]-1까지이다.
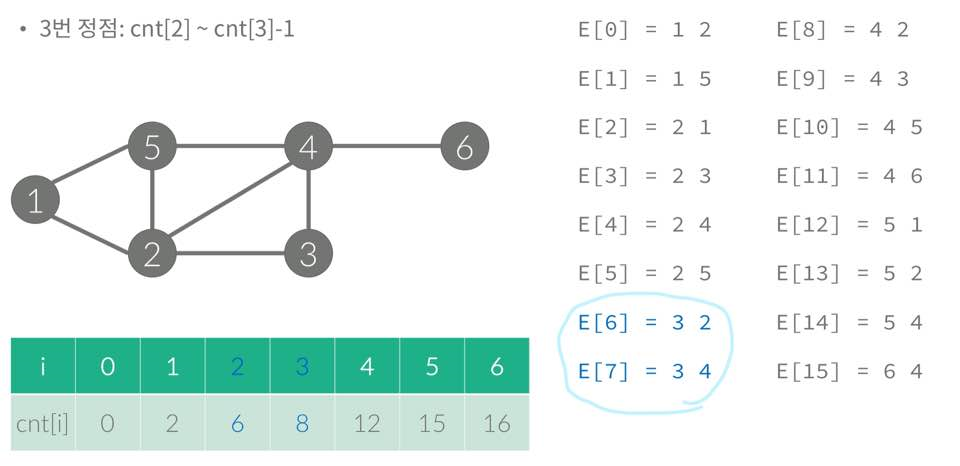
- 한 개의 정점과 연결된 모든 간선 찾는데 걸리는 시간 = O(차수)
<13023번 / ABCDE>
총 N명의 친구 관계가 주어졌을 때 다음과 같은 친구 관계가 존재하는지 구하는 문제
: A-B-C-D-E

요러케 구하면 된다고 한다. 흠 사실 인강 들으면서 이해 못함ㅋㅋㅋ
그래서 직접 구현하면서 이해해보려구~
1) 저기서 a-b, c-d가 친구인건 간선리스트로 찾는다. 그건 간선리스트가 모든 간선을 순회해보기엔 가장 좋은 자료구조기 때문인거지~
2) 그리고 c-d는 인접행렬로 찾는데, 이건 c-d 간선이 있는지만 확인하면 되는데 (u,v) 간선의 유무 찾기에는 인접행렬이 가장 좋은 거지 -> O(1)
3) 마지막으로 d-e는 인접리스트로 찾는데 이건 뭐 다 써보려고 하는거 아닐까? 간선리스트랑 시간복잡도가 똑같긴한데 일단 이렇게 구현해보는걸루
엥 뭐야 이렇게 복사하니까 훨씬 이뿌네... 뭐 암튼 이런식으로 구현했다. 대충 이해는 가는 느낌이다
추후 추가 공부 필요!!
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
bool a[2000][2000]; //인접행렬
vector<int> g[2000]; //인접리스트
vector<pair<int, int>> edges;//간선리스트
int main(void)
{
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i++)
{
int from, to; //친구관계 입력을 위한 변수
cin >> from >> to;
edges.push_back({ from,to });
edges.push_back({ to, from });
a[from][to] = a[to][from] = true;
g[from].push_back(to);
g[to].push_back(from);
}
m *= 2;
for (int i = 0; i < m; i++)
{
for (int j = 0; j < m; j++)
{
int A = edges[i].first;
int B = edges[i].second;
int C = edges[j].first;
int D = edges[j].second;
if (A==B || A==C ||A==D||B==C||B==D||C==D)
{
continue;
}
if (a[B][C]!=true)
{
continue;
}
for (int E : g[D])
{
if (A == E || B == E || C == E || D == E)
{
continue;
}
cout << 1 << '\n';
return 0;
}
}
}
cout << 0 << '\n';
return 0;
}
------------------------------------------------------------------------------------------------
강의 나머지 부분은 다음 글에 써야지😋
'코딩테스트 > 알고리즘 기초 강의' 카테고리의 다른 글
| 2강 - 그래프 1 (2) _ 그래프의 탐색 (0) | 2020.12.30 |
|---|---|
| 1강 브루트 포스 - 재귀 (0) | 2020.09.03 |
| 1강 브루트 포스 - 순열 (0) | 2020.09.01 |
| 1강 브루트 포스 - N과 M (0) | 2020.08.29 |
| 1강 브루트 포스 - 건너 뛰며 해보기 (0) | 2020.08.28 |




댓글