요번 문제도 이전에 푼 적이 있지만, 이전 풀이가 불친절(?)한 관계로 보다 자세하게 풀이를 남기려고 한다😅
[문제]
https://school.programmers.co.kr/learn/courses/30/lessons/43105
코딩테스트 연습 - 정수 삼각형
[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] 30
school.programmers.co.kr
[이전 풀이]
https://yummy0102.tistory.com/395
[DP] 정수 삼각형 - JAVA
https://school.programmers.co.kr/learn/courses/30/lessons/43105 프로그래머스 코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는
yummy0102.tistory.com
다음은 내가 해당 문제 풀이를 고민하면서 정리했던 필기이다!
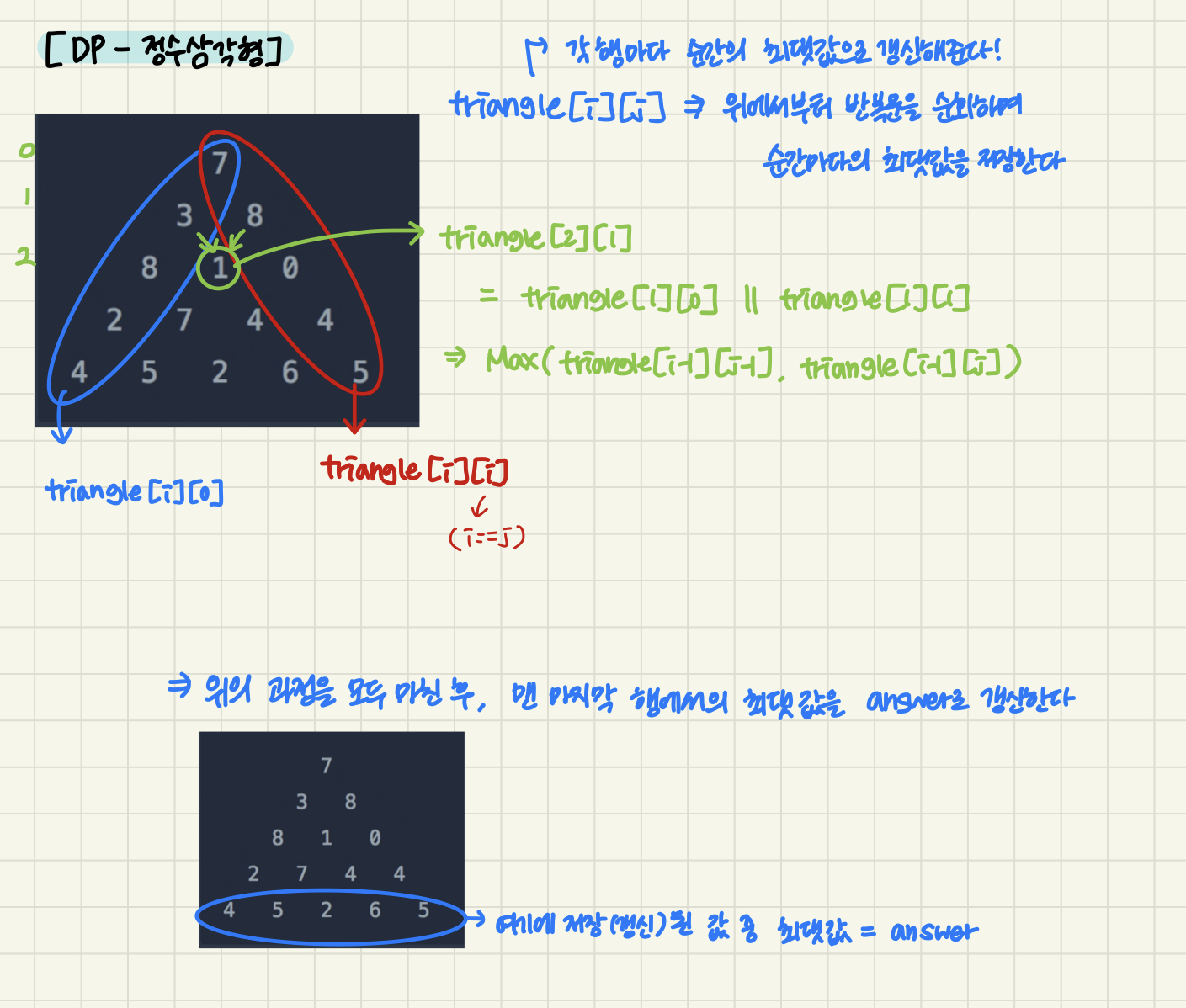
이제 위의 필기를 차례대로 풀어서 다시 고민해보자!
🤔 DP를 위한 memoization 배열 정의하기
DP 문제 특성 상, 이전 값을 저장해 둘 배열을 정의할 필요가 있다
해당 문제의 경우, 삼각형의 꼭대기부터 바닥까지 각 행의 숫자를 하나씩 더했을 때 나올 수 있는 최댓값을 구해야 한다
따라서 주어진 이차원배열인 int[][] triangle 을 사용할 것이다!
triangle[i][j] 에는 해당 위치까지 삼각형의 숫자를 위에서부터 더했을 때 최댓값을 저장한다!
🤔 경우의 수 나눠보기
우선 삼각형의 위에서 아래로 내려오면서 숫자를 선택해서 더할 수 있는 경우의 수를 나눠보자
스포하자면 총 3가지의 경우의 수가 존재한다!
1. triangle[i][0]

첫번째는 위와 같이 맨 왼쪽의 숫자를 더하는 경우이다
위의 경우에는 아래로 내려오면서 더할 수 있는 경우가 오직 바로 위의 숫자를 더하는 경우밖에 없다
따라서 열의 첫번째 숫자인 경우, 그냥 바로 위의 행, 같은 열의 숫자를 더해주면 된다
이를 점화식으로 표현하면 다음과 같다
// j==0 인 경우
triangle[i][j] += triangle[i-1][j]
2. triangle[i][i]

두번째도 첫번째와 비슷한 경우로, 맨 마지막 열 숫자인 경우이다
이 또한 위에서 아래로 내려오면서 더할 수 있는 숫자가 바로 위의 숫자 뿐이다
따라서 각 행의 맨 마지막 열의 숫자의 경우, 바로 위의 숫자를 더해주면 된다
이를 점화식으로 표현하면 다음과 같다
// i==j 인 경우
triangle[i][j] += triangle[i-1][j-1]
3. max(triangle[i-1][j-1], triangle[i-1][j])
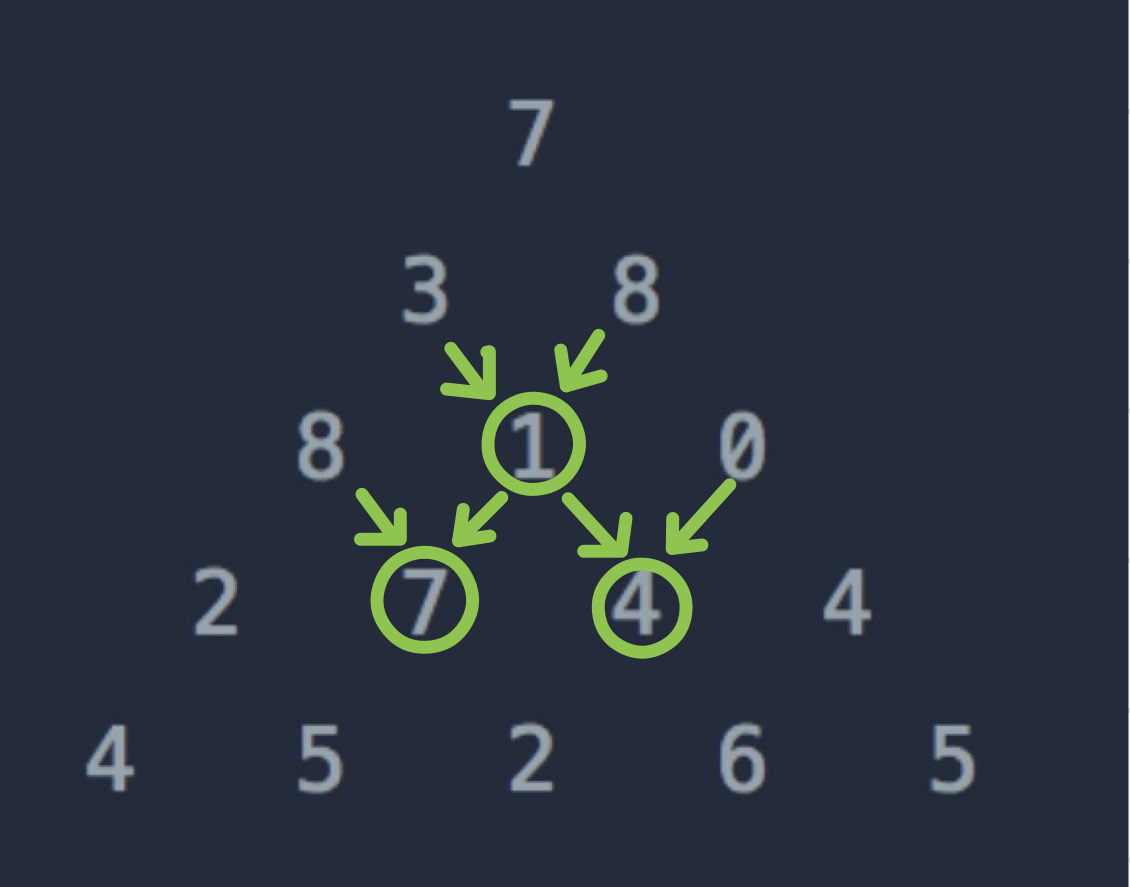
마지막은 위와 같이 두 개의 숫자 중 최댓값을 선택해서 더해주는 경우이다
가운데에 위치한 숫자의 경우, 왼쪽 위와 오른쪽 위의 숫자 중 하나를 선택해서 더할 수 있다
따라서 두 개의 숫자 중, 최댓값을 선택해서 더해주면 된다
이를 점화식으로 표현하면 다음과 같다
// else
triangle[i][j] += Math.max(triangle[i-1][j-1], triangle[i-1][j])
🤔 정답 도출하기
이제 위의 과정을 통해 삼각형의 모든 위치에서의 최댓값을 구했다면, 정답을 구할 차례이다
정답은 삼각형의 바닥의 숫자들 중에서 최댓값을 선택하면 된다

따라서 반복문을 통해 int[][] triangle에 저장된 맨 마지막 행의 숫자 중 최댓값을 return하면 된다!
다음은 최종 자바 코드이다!
[자바 코드]
class Solution {
public int solution(int[][] triangle) {
int answer = 0;
int n = triangle.length;
for(int i=1;i<n;i++) {
for(int j=0;j<=i;j++) {
int temp = triangle[i][j];
if(j==0) {
temp += triangle[i-1][j];
}
else if(i==j) {
temp += triangle[i-1][j-1];
} else {
temp += Math.max(triangle[i-1][j-1], triangle[i-1][j]);
}
triangle[i][j] = temp;
}
}
for(int i=1;i<n;i++) {
if(answer<triangle[n-1][i]) {
answer = triangle[n-1][i];
}
}
return answer;
}
}
사실 이번에도 이전 풀이와 코드는 동일하다
그래도 중요한건 뭐다? 다시 봐도 기억날 정도의 자세한 풀이과정을 추가했다는 것이다~~
그럼 안녕!
'코딩테스트 > 프로그래머스' 카테고리의 다른 글
| [DP] 도둑질 - JAVA (0) | 2023.03.28 |
|---|---|
| [DP] N으로 표현 - JAVA (version 2) (0) | 2023.03.10 |
| [연습문제] 귤 고르기 - JAVA (0) | 2022.12.22 |
| [연습 문제] 디펜스 게임 - JAVA (0) | 2022.12.19 |
| [완전탐색] 모음사전 - JAVA (0) | 2022.12.15 |


댓글