DFS 동작 과정
- DFS는 탐색을 위해서 사용되는 탐색 알고리즘이다
- 이제 DFS의 구체적인 동작 과정을 확인해보자!
- DFS는 특정한 경로로 탐색하다가 특정한 상황에서 최대한 깊숙이 들어가서 노드를 방문한 후, 다시 돌아가 다른 경로로 탐색하는 알고리즘이다
- DFS는 스택 자료구조를 이용하며 구체적인 동작 과정은 다음과 같다
- 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다
- 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다
- 2번의 과정을 더 이상 수행할 수 없을 떄까지 반복한다
*'방문 처리'는 스택에 한번 삽입되어 처리된 노드가 다시 삽입되지 않게 체크하는 것을 의미한다. 방문 처리를 함으로써 각 노드를 한번씩만 처리할 수 있다
- 이제 예시를 통해 DFS의 동작 과정을 확인해보자
- 노드 1을 시작 노드로 설정하여 DFS를 이용해 탐색을 진행한다고 하자
- DFS는 이름 그대로 '깊이 우선 탐색'으로 가장 깊숙이 위치하는 노드에 닿을 때까지 탐색하면 된다!
- 일반적으로 인접한 노드 중에서 방문하지 않은 노드가 여러 개 있으면 번호가 낮은 순서부터 처리된다
먼저 그림에서는 방문 처리된 노드는 회색으로, 현재 처리하는 스택의 최상단 노드는 하늘색으로 표현했다!
(참고로 왼쪽 네모는 스택임!)

STEP 1) 시작 노드인 1을 스택에 삽입하고 방문 처리를 한다

STEP 2) 스택의 최상단 노드인 1에 방문하지 않은 인접 노드 2, 3, 8이 있다. 이 중에서 가장 작은 노드인 2를 스택에 넣고 방문 처리를 한다

STEP 3) 스택의 최상단 노드인 2에 방문하지 않은 인접 노드 7이 있다. 따라서 7번 노드를 스택에 넣고 방문 처리를 한다

STEP 4) 스택의 최상단 노드인 7에 방문하지 않은 인접 노드 6과 8이 있다. 이 중에서 가장 작은 노드인 6을 스택에 넣고 방문 처리를 한다

STEP 5) 스택의 최상단 노드인 6에 방문하지 않은 인접 노드가 없다. 따라서 스택에서 6번 노드를 꺼낸다

STEP 6) 스택의 최상단 노드인 7에 방문하지 않은 인접 노드 8이 있다. 따라서 8번 노드를 스택에 넣고 방문 처리를 한다
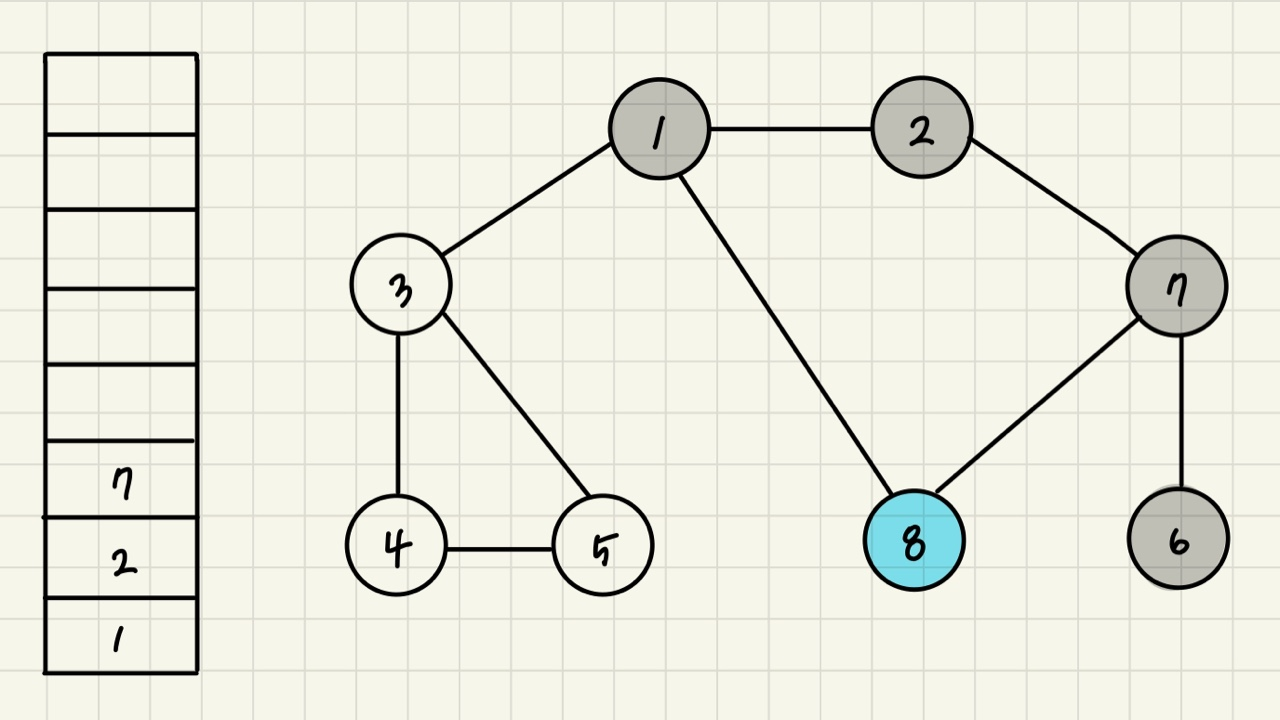
STEP 7) 스택의 최상단 노드인 8에 방문하지 않은 인접 노드가 없다. 따라서 스택에서 8번 노드를 꺼낸다.

STEP 8) 스택의 최상단 노드인 7에 방문하지 않은 인접 노드가 없다. 따라서 스택에서 7번 노드를 꺼낸다.

STEP 9) 스택의 최상단 노드인 2에 방문하지 않은 인접 노드가 없다. 따라서 스택에서 2번 노드를 꺼낸다.

STEP 10) 스택의 최상단 노드인 1에 방문하지 않은 인접 노드 3을 스택에 넣고 방문 처리한다.

STEP 11) 스택의 최상단 노드인 3에 방문하지 않은 인접 노드 4와 5가 있다. 이 중에서 가장 작은 노드인 4를 스택에 넣고 방문 처리를 한다.

STEP 12) 스택의 최상단 노드인 4에 방문하지 않은 인접 노드 5가 있다. 따라서 5번 노드를 스택에 넣고 방문 처리한다.
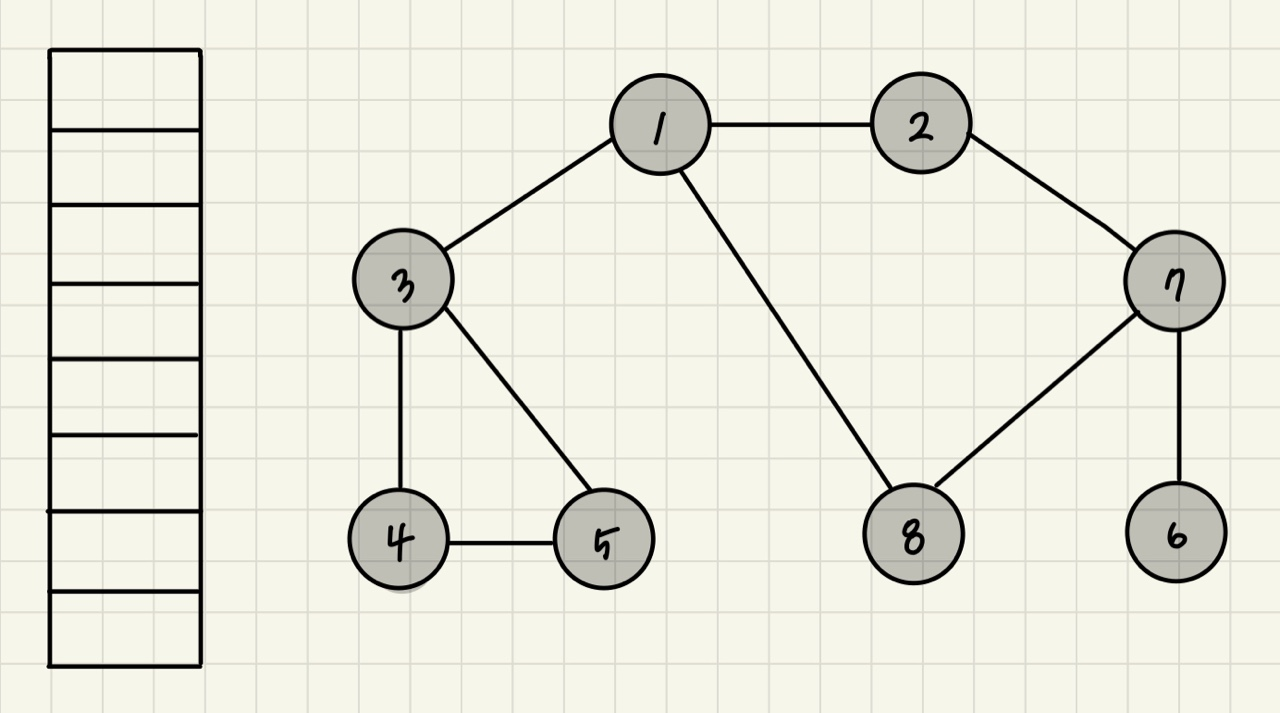
STEP 13) 남아 있는 노드에 방문하지 않은 인접 노드가 없다. 따라서 모든 노드를 차례대로 꺼내면 다음과 같다.
결과적으로 노드의 탐색 순서 (스택에 들어간 순서)는 다음과 같다!
1 -> 2 -> 7 -> 6 -> 8 -> 3 -> 4 -> 5
깊이 우선 탐색 알고리즘인 DFS는 스택 자료구조에 기초한다는 점에서 구현이 간단하다
실제로는 스택을 쓰지 않아도 되며, 탐색을 수행함에 있어서 데이터의 개수가 N개인 경우
O(N)의 시간이 소요된다는 특징이 있다
또한 DFS는 스택을 이용하는 알고리즘이기 때문에 실제 구현은 재귀 함수를 이용했을 때 매우 간결하게 구현할 수 있다
아래는 DFS를 구현한 파이썬 코드와 C++ 코드이다!
파이썬 코드)
# DFS 함수 정의
def dfs(graph, v, visited):
# 현재 노드를 방문 처리
visited[v] = True
print(v, end=' ')
# 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
# 각 노드가 연결된 정보를 리스트 자료형으로 표현(2차원 리스트)
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
# 각 노드가 방문된 정보를 리스트 자료형으로 표현(1차원 리스트)
visited = [False] * 9
# 정의된 DFS 함수 호출
dfs(graph, 1, visited)visited 리스트를 통해 방문 처리를 한다 -> true면 방문 처리된것
graph에는 각 노드별로 연결된 노드를 저장한다 -> graph[1]은 1번 노드에 연결된 노드이다
여기서 연산을 편하게 하기 위해 graph에 0번은 비워두고, visited도 9개로 초기화한다
또한 dfs는 재귀 함수로 구현했는데, dfs에 매개 변수 v가 현재 최상단 노드니까 그 노드를 방문 처리하고 반복해서 해당 노드와 연결된 노드를 확인한다.
그 때 vistied가 fasle면 방문하지 않은 거니까 다시 dfs를 호출한다.
아래는 파이썬 dfs 코드 결과화면이다

C++ 코드)
#include <iostream>
#include <vector>
#include <stdio.h>
using namespace std;
bool visited[9];
vector<int> graph[3];
void dfs(int v)
{
//현재 노드를 방문 처리
visited[v]=true;
cout<<v<<" ";
//현재 노드와 연결된 다른 노드를 재귀적으로 방문
for(int i=0;i<graph[v].size();i++)
{
int x = graph[v][i];
if(!visited[x]) dfs(x);
}
}
int main()
{
// 노드 1에 연결된 노드 정보 저장
graph[1].push_back(2);
graph[1].push_back(3);
graph[1].push_back(8);
// 노드 2에 연결된 노드 정보 저장
graph[2].push_back(1);
graph[2].push_back(7);
// 노드 3에 연결된 노드 정보 저장
graph[3].push_back(1);
graph[3].push_back(4);
graph[3].push_back(5);
// 노드 4에 연결된 노드 정보 저장
graph[4].push_back(3);
graph[4].push_back(5);
// 노드 5에 연결된 노드 정보 저장
graph[5].push_back(3);
graph[5].push_back(4);
// 노드 6에 연결된 노드 정보 저장
graph[6].push_back(7);
// 노드 7에 연결된 노드 정보 저장
graph[7].push_back(2);
graph[7].push_back(6);
graph[7].push_back(8);
// 노드 8에 연결된 노드 정보 저장
graph[8].push_back(1);
graph[8].push_back(7);
dfs(1);
return 0;
}c++에서는 vector<int>로 graph를 선언하고 이는 3개의 노드를 갖도록 구현한다
그리고 graph에 연결된 노드를 저장할 때는 push_back을 통해 구현한다
알고리즘은 파이썬과 동일하다
다른 점은 graph와 visitied를 전역 변수로 선언해서 따로 dfs 함수에 매개변수로 넘겨주지 않아도 되는거 정도?
+추가)
자바코드)
import java.util.*;
public class Main {
public static boolean[] visited = new boolean[9];
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// DFS 함수 정의
public static void dfs(int x) {
// 현재 노드를 방문 처리
visited[x] = true;
System.out.print(x + " ");
// 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for (int i = 0; i < graph.get(x).size(); i++) {
int y = graph.get(x).get(i);
if (!visited[y]) dfs(y);
}
}
public static void main(String[] args) {
// 그래프 초기화
for (int i = 0; i < 9; i++) {
graph.add(new ArrayList<Integer>());
}
// 노드 1에 연결된 노드 정보 저장
graph.get(1).add(2);
graph.get(1).add(3);
graph.get(1).add(8);
// 노드 2에 연결된 노드 정보 저장
graph.get(2).add(1);
graph.get(2).add(7);
// 노드 3에 연결된 노드 정보 저장
graph.get(3).add(1);
graph.get(3).add(4);
graph.get(3).add(5);
// 노드 4에 연결된 노드 정보 저장
graph.get(4).add(3);
graph.get(4).add(5);
// 노드 5에 연결된 노드 정보 저장
graph.get(5).add(3);
graph.get(5).add(4);
// 노드 6에 연결된 노드 정보 저장
graph.get(6).add(7);
// 노드 7에 연결된 노드 정보 저장
graph.get(7).add(2);
graph.get(7).add(6);
graph.get(7).add(8);
// 노드 8에 연결된 노드 정보 저장
graph.get(8).add(1);
graph.get(8).add(7);
dfs(1);
}
}
지금까지 DFS(깊이 우선 탐색) 알고리즘을 공부했다!
다음으로는 BFS(너비 우선 탐색) 알고리즘에 대해 공부해보자!!
'코딩테스트 > 이코테' 카테고리의 다른 글
| [CH5 DFS/BFS] 음료수 얼려 먹기 (0) | 2021.12.25 |
|---|---|
| [CH5 DFS/BFS] 탐색 알고리즘 DFS/BFS (3) (0) | 2021.12.22 |
| [CH5 DFS/BFS] 탐색 알고리즘 DFS/BFS (1) (0) | 2021.12.21 |
| [CH5 DFS/BFS] 꼭 필요한 자료구조 기초 (0) | 2021.12.20 |
| [CH4 구현] 게임 개발 (0) | 2021.12.09 |




댓글