🖐 최선, 평균, 최악의 경우
- 동일한 알고리즘도 입력되는 데이터에 따라 다른 실행 시간을 보일 수 있다
- 예를 들어 정렬을 하는 알고리즘에 대부분 정렬이 완료되어 있는 데이터를 입력한다면 뒤죽박죽 섞여 있는 데이터 집합보다 더 빨리 정렬이 완료될 것이다
- 따라서 알고리즘의 효율성은 입력되는 데이터의 집합에 따라 3가지의 경우로 나누어 평가할 수 있다
- 최선의 경우 (Best Case) : 실행 시간이 가장 적은 경우를 말한다
- 평균의 경우 (Average Case) : 모든 입력을 고려하고 각 입력이 발생하는 확률을 고려한 평균 수행 시간을 말한다
- 최악의 경우 (Worst Case) : 알고리즘의 수행 시간이 가장 오래 걸리는 경우
- 평균적인 경우의 실행 시간이 가장 측정하기 좋아보이지만, 광범위한 데이터 집합에 대하여 알고리즘을 적용시켜 평균값을 계산하는 것은 매우 어려울 수 도 있다
- 따라서 시간 복잡도의 척도를 계산할 때는 최악의 경우로 사용한다
점근적 표기법
| 빅 오(Big-O) 표기법 | 점근적 상한에 대한 표기 (worst case) | ex) O(n²) |
| 빅 세타(Big-θ) 표기법 | 상한과 하한의 평균에 대한 표기 (average case) | ex) θ(n²) |
| 빅 오메가(Big-Ω) 표기법 | 점근적 하한에 대한 표기 (best case) | ex) Ω(n²) |
- 빅 세타와 빅 오메가는 원하는 효율성을 정확하게 나타내지 못하기 때문에 빅오 표기법이 주로 사용된다
빅-오(Big-O) 표기법
- 시간 복잡도는 일반적으로 'Big-O' 표기법으로 나타낸다
- 빅오 표기법은 점근적 표기법(Asymptotic Notation)의 하나로 Landau symbol 이라고 부르기도 하며 알고리즘의 효율성을 나타낼 때 사용한다
- 빅-오 표기법은 최악의 경우(worst case)를 계산하는 방식이다

- 연산 횟수가 다항식으로 표현될 경우, 위와 같이 최고차항을 제외한 모든 항과 최고차항의 계수를 제외시켜 나타낸다
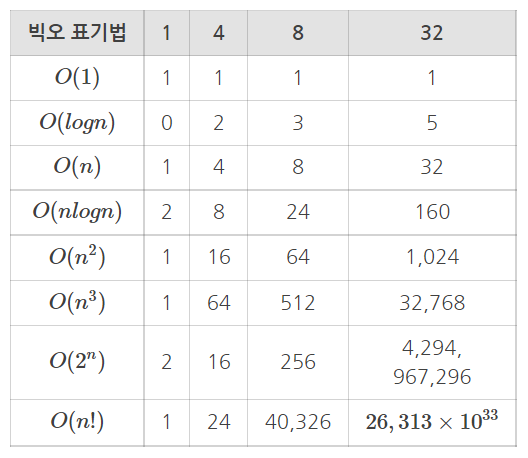
빅오 표기법의 성능 비교

위의 그래프는 시간 복잡도 그래프로, 여기서 n은 입력되는 데이터 개수를 의미한다
1) O(1) : Constant (상수 시간)
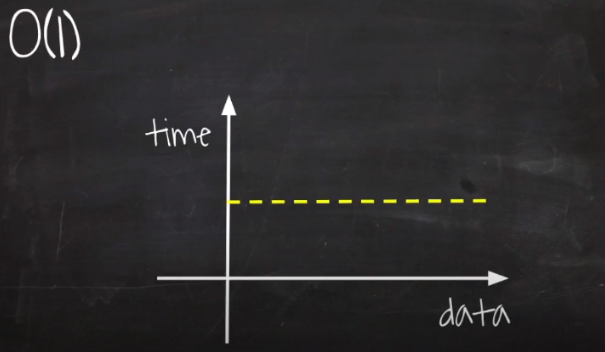
- 입력 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘을 나타낸다
- 데이터가 얼마나 증가하든 성능에 영향을 거의 미치지 않는다
- 스택의 Push, Pop 연산 등이 해당된다
2) O(log₂ n) : Logarithmic (로그 시간)
- 입력 데이터의 크기가 커질수록 처리 시간이 로그(log: 지수 함수의 역함수) 만큼 짧아지는 알고리즘이다
- 만약에 데이터가 10배가 되면, 처리 시간은 2배가 된다
- 이진 탐색이 대표적이며, 재귀가 순기능으로 이루어지는 경우도 해당된다
3) O(n) : Linear (선형 시간)
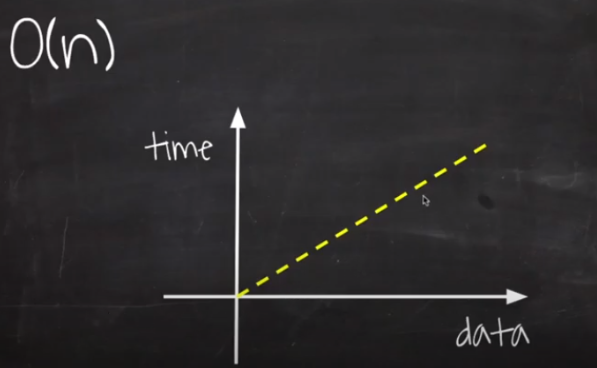
- 입력 데이터의 크기에 비례해 처리 시간이 증가하는 알고리즘이다.
- 만약 데이터가 10배가 되면, 처리 시간도 10배가 된다
- 대표적인 예시로는 1차원 for문이 있다
4) O(n log₂ n) : Linear-Logarithmic (선형 로그 시간)

- 데이터가 많아질수록 처리시간이 로그(log) 배만큼 더 늘어나는 알고리즘이다
- 만약 데이터가 10배가 되면, 처리 시간은 약 20배가 된다
- 정렬 알고리즘 중 병합 정렬(merge sort), 퀵 정렬(quick sort), 힙 정렬(heap sort)이 대표적이다
5) O(n²) : quadratic (이차 시간)

- 데이터가 많아질수록 처리시간이 급수적으로 늘어나는 알고리즘이다
- 만약 데이터가 10배가 되면, 처리 시간은 최대 100배가 된다
- 이중 루프(n² matrix / for문)가 대표적이며 단, m이 n보다 작을 때는 반드시 O(nm)로 표시하는 것이 바람직하다
- 이외에도 삽입 정렬(insertion sort), 거품 정렬(bubble sort), 선택 정렬(selection sort) 등이 해당된다
6) O(2ⁿ) : Exponential (지수 시간)

- 데이터량이 많아질수록 처리시간이 기하급수적으로 늘어나는 알고리즘이다
- 대표적으로 피보나치 수열이 있으며, 재귀가 역기능을 할 경우도 해당된다


📌 시간 복잡도에 따른 성능
(faster) O(1) < O(log n) < O(nlog n) < O(n²) < O(2ⁿ) (slower)
오른쪽으로 갈수록 효율성이 떨어진다!
빅오 표기법의 특징
1. 상수항 무시
- 빅오 표기법은 데이터의 입력값(n)이 충분히 크다고 가정하고 있고, 알고리즘의 효율성 또한 데이터 입력값(n)의 크기에 따라 영향을 받기 때문에 상수항과 같이 사소한 부분은 무시한다
- ex) O(2N)의 경우 O(N)으로 상수항은 무시하고 표기한다
2. 영향력 없는 항 무시
- 빅오 표기법은 데이터 입력값(n)의 크기에 따라 영향을 받기 때문에 가장 영향력이 큰 항 이외의 영향력 없는 항들은 무시하고 표기한다
- ex) O(n²+2n+1) 은 O(n²) 와 같이 영향력이 큰 항인 n² 만 남겨두고 나머지 항들은 무시한다
🎯 알고리즘의 간단하게 Big-O 계산하기
- 일일이 primitive operation을 세는 것은 의미가 없다
- 루프 밖에 있는 단순 연산들은 결국 상수항이라 제외되고, 루프 안에 여러 개의 연산이 있다고 하더라도 가장 큰 차수 외에는 각 항의 계수를 포함한 모든 것이 무시된다
- 즉, Big-O 표기법은 루프의 차수(깊이)와 직결된다
- 따라서 루프와 recursion 횟수만 확인하면 된다
- 만약 n에 대한 loop가 1개면 O(n), 2개면 O(n²)라고 할 수 있다
- 조심할 부분은 만약 위의 알고리즘 내의 두 번째 루프에서 루프의 limit이 i대신 j가 들어갔고, n 대신 m이 새로운 변수라면 O(n²)이 아니라 O(mn)이 된다!
- 간단히 생각하면 n과 관련된 그 어떤 변수를 루프 안에 쓰더라도, 루프가 하나면 O(n)으로 나타내면 된다
- 단, O(logn)이나 O(n logn)의 경우 해당되는 알고리즘의 형태들이 다르다
- O(n logn) : 배열의 정렬(array sorting) 중 힙 정렬(heap sorting) 이 해당한다
참고)
https://noahlogs.tistory.com/27
빅오 표기법 (big-O notation) 이란
컴퓨터 과학(Computer Science) 에서 알고리즘은 어떠한 문제를 해결하기 위한 방법이고, 어떠한 문제를 해결 하기 위한 방법은 다양하기 때문에 방법(알고리즘) 간에 효율성을 비교하기 위해 빅오(
noahlogs.tistory.com
[자료구조] 빅오 표기법(Big-O notation)이란?
빅 오 표기법(Big-O notation)의 정의 Big-O(또는 Big-Oh) notation은 알고리즘의 시간 복잡도를 나타내는 표기법이며, O(f(n))으로 나타낸다. 알고리즘의 시간 복잡도 알고리즘의 복잡도를 판단하는 척도
holika.tistory.com
https://choonse.com/2022/01/29/763/
빅오 표기법(Big O notation)을 알아보자 - WORLD IS WIDE
빅오(Big O) 표기법은 점근적 표기법(Asymptotic Notation)의 하나로 Landau symbol이라고 부르기도 하며, 알고리즘의 효율성(시간 복잡도)를 나타낼 때 사용합니다.
choonse.com
https://zoozoozoo.tistory.com/186
시간 복잡도 계산하기 Big-O 표기법
Big-O 표기법은 무엇일까? - 알고리즘의 성능을 수학적으로 표현해주는 표기 법이다. - 알고리즘의 시간과 공간 복잡도를 표현할 수 있다. - 알고리즘의 실제 러닝 타임을 표시하기보다는 데이터
zoozoozoo.tistory.com
'야미스터디 > Algorithm' 카테고리의 다른 글
| 제자리 정렬 & 안정 정렬 (1) | 2023.07.13 |
|---|---|
| [알고리즘] DFS/BFS 📌 (0) | 2022.10.02 |
| [알고리즘] Tree 구조 📌 (1) | 2022.09.13 |
| [알고리즘] 동적 계획법(DP) 📌 (0) | 2022.08.28 |
| [알고리즘] 시간 복잡도 vs 공간 복잡도 📌 (2) | 2022.08.26 |




댓글