Tree구조

- Tree 구조란 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조이다
- 트리는 위와 같이 나무를 거꾸로 뒤집어 놓은 모양과 유사하다고 하여 붙여진 이름이다
- 또한 트리 내에 다른 하위 트리가 있고, 그 하위 트리 안에 또 다른 하위 트리가 있는 재귀적 자료구조읻
- 대표적인 예시로는 컴퓨터의 directory 구조가 있다

Tree 구조 용어
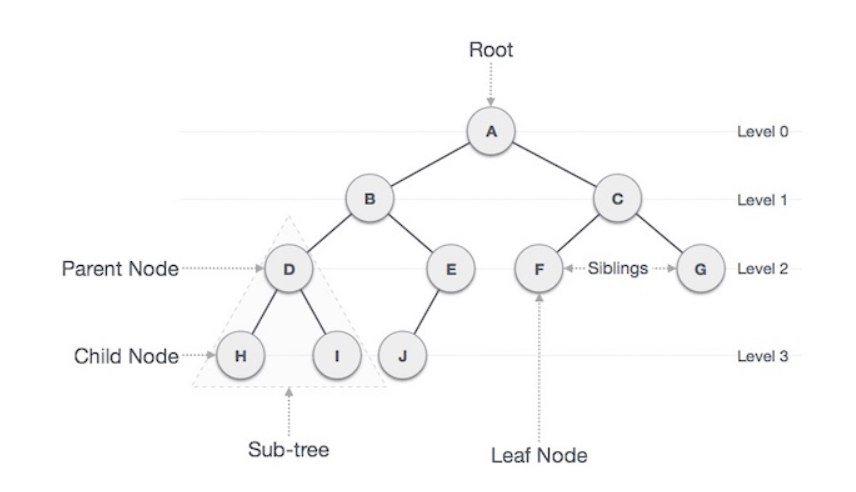
1) 노드 (Node)
- 트리를 구성하고 있는 기본 요소
- 노드에는 키 또는 값과 하위 노드에 대한 포인터를 가지고 있다
- 위의 그림에서 A, B, C, D, ..., I, J 까지 모두 노드이다
2) 간선 (Edge)
- 노드와 노드 간의 연결선
- 위의 그림에서 노드 간을 연결하는 직선이다
3) 루트 노드 (Root Node)
- Tree 구조에서 부모가 없는 최상위 노드
- 위의 그림에서는 A 노드가 루트 노드가 된다
4) 부모 노드 (Parent Node)
- 자식 노드를 가진 노드
- ex) 노드 H, I의 부모 노드는 D가 된다
5) 자식 노드 (Child Node)
- 부모 노드의 하위 노드
- ex) 노드 D의 자식 노드는 H, I 노드이다
6) 형제 노드 (Sibiling Node)
- 같은 부모를 갖는 노드
- ex) 노드 H와 I는 같은 부모를 갖는 형제 노드이다
7) 리프 노드 (Leaf Node)
- 자식 노드가 없는 최하위 노드
- 외부 노드 (external node, outer node) 또는 단말 노드 (terminal node) 라고도 부른다
- ex) H, I, J, F, G 노드
8) 가지 노드 (Branch Node)
- 자식 노드를 하나 이상 갖는 노드
- 내부 노드 (internal node, inner node), 비 단말 노드 (non-terminal node)
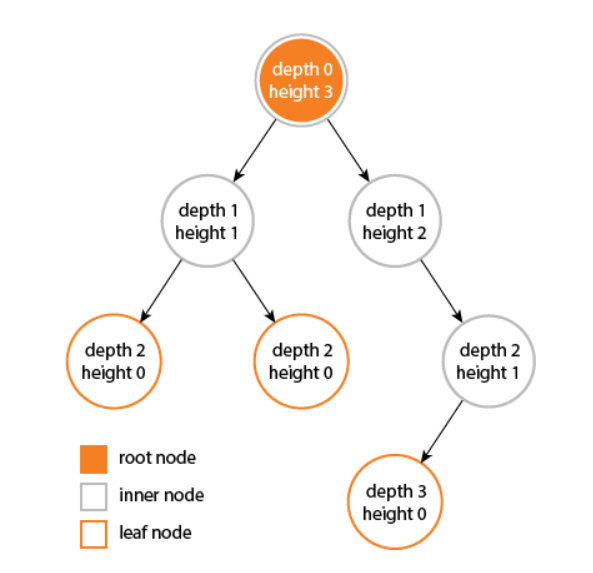
9) 깊이 (depth)
- 루트에서 어떤 노드까지의 간선(Edge) 수
- Level 이라고도 부른다
- 루트 노드의 깊이는 0이 된다
- ex) 노드 D의 깊이 = 2
10) 높이 (height)
- 어떤 노드에서 리프 노드까지 가장 긴 경로의 간선(Edge) 수
- 리프 노드의 높이는 0이 된다
- ex) 노드 A의 높이 = 3
11) 차수 (Degree)
- 노드의 자식(가지) 수, 하위 트리 개수
- 리프 노드의 degree는 0이다
- 트리의 차수(degree of tree)는 트리의 최대 차수로, 위의 그림에선 2가 된다
- ex) 노드 A의 degree는 2가 된다
12) Path
- 한 노드에서 다른 한 노드에 이르는 길 사이에 놓여있는 노드들의 순서
- ex) 노드 A - 노드 H의 path = A - B - D - H
13) Path Length
- 해당 경로에 있는 총 노드의 수
- ex) 노드 A - 노드 H의 Path Length = 4
14) Size
- 자신을 포함한 자손의 노드 수
- ex) 노드 B의 size = 6
15) Level
- 트리의 특정 깊이를 갖는 노드의 집합
- 루트 노드의 Level은 0이다
- ex) Level 2 = 노드 B, 노드C
16) Width
- 레벨에 있는 노드 수
- ex) Level 2의 width = 4
17) Breadth
- 리프 노드의 수
- ex) Breadth = 5
18) Distance
- 두 노드 사이의 최단 경로에 있는 간선(Edge)의 수
- ex) 노드 D와 J의 Distance = 3
19) Order
- 부모 노드가 가질 수 있는 최대 자식의 수
- ex) Order 3 : 부모 노드는 최대 3명의 자식을 가질 수 있다
20) 숲 (Forest)

- 여러 개의 트리가 모여 있는 것을 의미한다
- 위 그림에서 루트 노드 A를 제거하면 B, C, D를 루트 노드로 하는 세 개의 트리가 있는 숲이 생긴다
Tree 특징

- 하나의 루트 노드와 0개 이상의 하위 트리로 구성된다
- 데이터를 순차적으로 저장하지 않는 비선형 자료구조이다
- 트리 내에 또 다른 트리가 있는 재귀적 자료구조이다
- 단순 순환(Loop)를 갖지 않고, 연결된 무방향 그래프 구조이다
- 노드 간에 부모 자식 관계를 갖고 있는 계층형 자료구조이며, 모든 자식 노드는 하나의 부모 노드만 갖는다
- 노드가 n개인 트리는 항상 n-1개의 간선(Edge)을 갖는다
Tree가 아닌 경우

- 위는 루트 노드가 2개(2번 노드, 8번 노드)이므로 트리가 아니다

- 6번 노드에는 부모 노드가 2개(5번 노드, 8번 노드)이고, 사이클이 형성되므로 트리가 아니다

- 트리의 노드는 self-loop가 존재하면 안되기 때문에 위 또한 트리가 아니다
Tree 종류
1) 편향 트리 (skew tree)
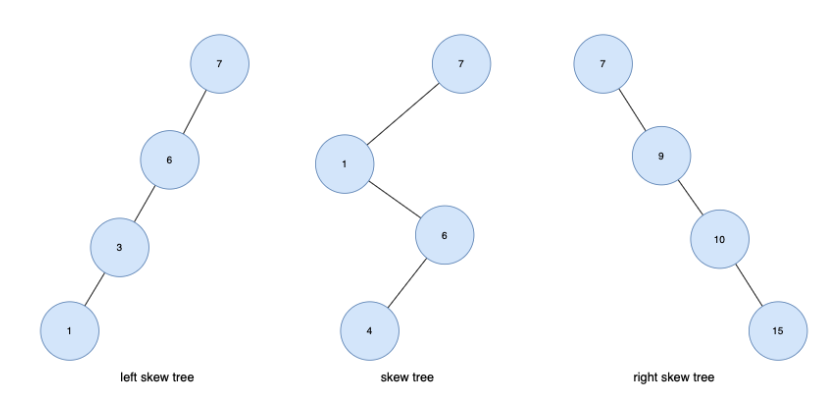
- 모든 노드들이 자식을 하나만 갖는 트리
- 왼쪽 방향으로 자식을 하나씩만 가지면 left skew tree, 오른쪽 방향으로 하나씩만 가지면 right skew tree라고 한다
2) 이진 트리 (Binary Tree)

- 각 노드의 차수(자식 노드)가 2 이하인 트리
- 모든 노드가 최대 2개의 서브 트리를 가지며, 서브 트리 또한 모두 이진 트리이다
- 즉, branch가 최대 2개인 노드로만 구성된다
2-1) 완전 이진 트리 (Complete Binary Tree)

- 완전 이진 트리는 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있다
- 마지막 레벨은 꽉 차 있지 않아도 되지만, 노드가 왼쪽에서 오른쪽으로 채워져야 한다
- 마지막 레벨 N에서 1 ~ 2N-1 개의 노드를 가질 수 있다
- 완전 이진 트리는 배열을 사용해 효율적으로 표현할 수 있다
2-2) 전 이진 트리 (Full Binary Tree)
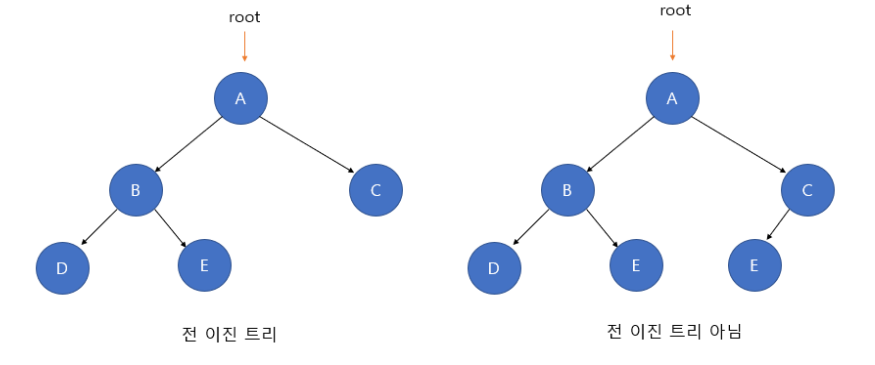
- 전 이진 트리는 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리이다
2-3) 포화 이진 트리 (Perfect Binary Tree)
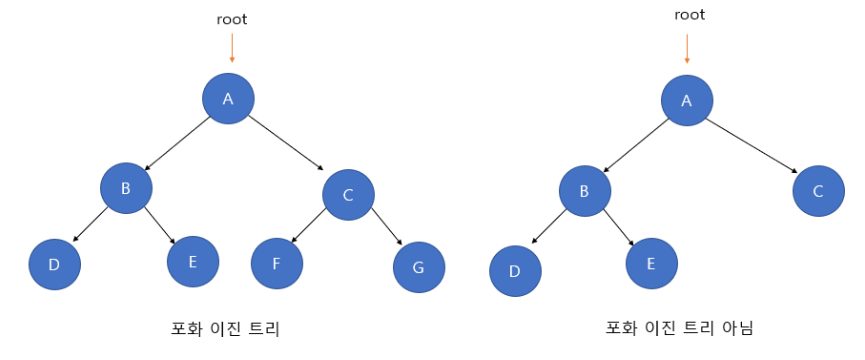
- 포화 이진 트리는 모든 레벨이 노드로 꽉 차 있는 트리를 말한다
- 전 이진 트리의 성질도 만족해야 한다 -> 즉, 모든 노드가 0개 혹은 2개의 자식 노드를 갖는다
- 모든 말단 노드가 동일한 깊이 또는 레벨을 갖는다
- 트리의 높이가 k일 때, 트리의 노드 개수가 정확히 2^k-1 개여야 한다
3) 이진 탐색 트리 (Binary Search Tree, BST)

- 이진 트리에 조건이 더해진 트리로, 순서화 된 이진 트리이다
- 왼쪽과 오른쪽 서브 트리 또한 이진 탐색 트리이다
- 이는 효율적인 탐색을 위해 고안된 트리이다
- 노드의 왼쪽 자식은 부모의 값보다 작은 값을 가져야 하며, 노드의 오른쪽 자식은 부모의 값보다 큰 값을 가져야 한다
- 즉, 모든 노드가 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드 의 순서대로 값이 크다
- 또한 부모 노드를 중심으로 작은 값은 왼쪽 자식 노드에 큰 값은 오른쪽 자식 노드에 존재해야 하므로, 이진 탐색 트리의 모든 노드의 데이터 값은 중복되는 값이 존재하면 안된다
- 즉, 데이터 값(노드의 key 값)은 유일해야 한다!
[ ex. 이진 탐색 트리 (BST) 예시 ]

- 이진 탐색 트리는 위와 같이 만들 수 있다
- BST를 통해 데이터를 효율적으로 검색(탐색)할 수 있다

- 원하는 값을 찾을 때까지 현재의 노드 값보다 찾고자 하는 값이 작으면 왼쪽으로 움직이고, 크면 오른쪽으로 움직인다
- 이런 방식으로 더 빠르게 찾을 수 있다
4) m 원 탐색 트리 (m-way search tree)
- 최대 m개의 서브 트리를 갖는 탐색 트리
- 이진 탐색 트리의 확장된 형태로, 높이를 줄이기 위해 사용된다
5) 균형 트리 (Balanced Tree, B-Tree)
- m 원 탐색 트리에서 높이 균형을 유지하는 트리
- height-balanced m-way tree라고도 부른다
Tree 순회
- 트리 자료구조에 포함된 노드들을 특정한 방법으로 한번씩 방문하는 방법
- 이를 통해 정보를 시각적으로 확인할 수 있다
1) 전위 순회 (Pre-order traversal)

- 루트 노드 -> 왼쪽 자식 -> 오른쪽 자식 순서대로 방문하는 순회 방법
2) 중위 순회 (In-order traversal)

- 왼쪽 자식 -> 루트 노드 -> 오른쪽 자식 순서로 방문하는 순회 방법
3) 후위 순회 (Post-order traversal)

- 왼쪽 자식 -> 오른쪽 자식 -> 루트 노드 순서로 방문하는 순회 방법
Tree의 사용 예시
1) 계층적 데이터 저장
- 트리는 데이터를 계층 구조로 저장하는 데 사용된다
- 파일이나 폴더는 계층적 트리 형태로 저장된다
2) 효율적인 검색 속도
- 효율적인 삽입, 삭제 및 검색을 위해 트리 구조를 사용한다
3) 힙 (Heap)
- 힙도 트리로 된 자료구조이다
4) 데이터베이스 인덱싱
- 데이터베이스 인덱싱을 구현하는데 트리를 사용한다
- ex) B-Tree, B+ Tree, AVL-Tree 등..
5) 트라이 (Trie)
- 사전을 저장하는데 사용되는 특별한 종류의 트리이다
- 각 노드에 문자를 저장하기 때문에 트리를 아래쪽으로 순회하면 단어 하나가 나온다
- 접두사를 빠르게 찾아보기 위한 방식으로, 모든 언어를 트라이에 저장해놓는다
- 유효한 단어 집합을 이용하는 많은 문제들은 트라이를 통해 최적화할 수 있다
💡 그래프 vs 트리

참고)
https://yoongrammer.tistory.com/68
[자료구조] 트리 (Tree)
목차 트리 (Tree) 트리 (Tree)란 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조입니다. 트리는 다음과 같이 나무를 거꾸로 뒤집어 놓은 모양과 유사합니다. 트리는 또한 트리 내에 다른 하
yoongrammer.tistory.com
https://jud00.tistory.com/entry/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%A6%ACTree%EB%9E%80
[자료구조] 트리(Tree)란
이번에는 자료구조 중 하나인 트리(Tree)에 대해서 정리하겠습니다. 가급적이면 쉽고 간단하게 설명할 예정이며, 더 깊고 많은 내용을 알고 싶으시다면 다른 블로그를 참고하시기 바랍니다 :) 트
jud00.tistory.com
https://hanamon.kr/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-tree-%ED%8A%B8%EB%A6%AC/
[자료구조] Tree 트리 - 하나몬
⚡️ Tree [그림] 트리 구조 예시 자료구조 Tree는 하나의 뿌리로부터 가지가 사방으로 뻗은 형태가 나무와 닮아서 트리 구조라고 부른다. 자료구조 Tree는 그래프의 여러 구조 중 무방향 그래프의
hanamon.kr
https://code-lab1.tistory.com/8
[자료구조] 트리(Tree)의 개념 | 이진 트리, 전 이진 트리, 완전 이진트리, 포화 이진 트리, 이진 탐
트리(Tree)의 개념 트리는 노드로 이루어진 자료구조로 스택이나 큐와 같은 선형 구조가 아닌 비선형 자료구조이다. 트리는 계층적 관계를 표현하는 자료구조이다. 트리는 다음과 같은 특징들을
code-lab1.tistory.com
https://coding-factory.tistory.com/231
[Algorithm] 트리(Tree)구조란 무엇인가?
트리(Tree)의 정의 트리는 정점(Node)과 선분(Branch)을 이용하여 사이클을 이루지 않도록 구성한 Graph의 특수한 형태이다. 가족의 계보(족보), 연산수식, 회사 조직 구조도, 히프등을 표현하기에 적
coding-factory.tistory.com
https://velog.io/@kimdukbae/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%A6%AC-Tree
[자료구조] 트리 (Tree)
사진의 출처 : 링크트리(Tree)는 그래프의 일종으로 정점과 간선을 이용하여 데이터의 배치 형태를 추상화한 자료구조이다.서로 다른 두 노드를 연결하는 길이 하나뿐인 그래프를 트리라고 부른
velog.io
https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html
[자료구조] 트리(Tree)란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
'야미스터디 > Algorithm' 카테고리의 다른 글
| 제자리 정렬 & 안정 정렬 (1) | 2023.07.13 |
|---|---|
| [알고리즘] DFS/BFS 📌 (0) | 2022.10.02 |
| [알고리즘] 동적 계획법(DP) 📌 (0) | 2022.08.28 |
| [알고리즘] 빅 오(Big-O) 표기법 📌 (0) | 2022.08.26 |
| [알고리즘] 시간 복잡도 vs 공간 복잡도 📌 (2) | 2022.08.26 |



